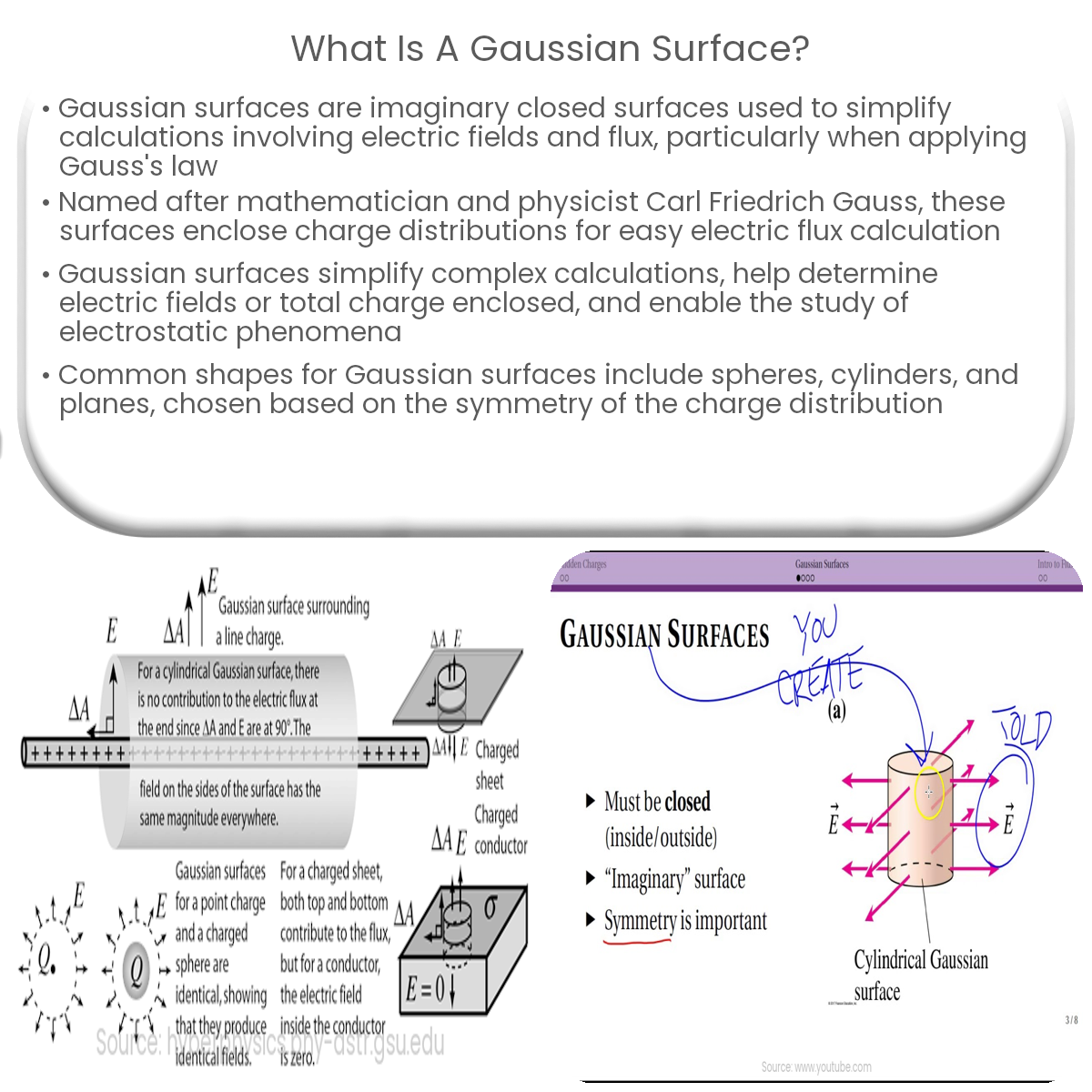
A Gaussian surface is an imaginary closed surface used to simplify electric field and flux calculations, particularly in applying Gauss’s law.
Introduction to Gaussian Surfaces
Gaussian surfaces are essential tools in the study of electrostatics, particularly when applying Gauss’s law. In this article, we will define Gaussian surfaces, explain their significance, and discuss their use in the context of Gauss’s law.
Definition of Gaussian Surfaces
A Gaussian surface is an imaginary closed surface used to simplify calculations involving electric fields and flux. It is named after the mathematician and physicist Carl Friedrich Gauss, who developed Gauss’s law. The purpose of a Gaussian surface is to enclose a charge distribution so that the electric flux through the surface can be easily calculated.
Significance of Gaussian Surfaces
Gaussian surfaces are significant for the following reasons:
- They simplify complex calculations involving electric fields and flux, especially when the charge distribution has a high degree of symmetry.
- They help in applying Gauss’s law effectively to determine the electric field or total charge enclosed within the surface.
- They enable the study of a wide range of electrostatic phenomena and their applications, such as capacitors and dielectric materials.
Gauss’s Law and Gaussian Surfaces
Gauss’s law states that the electric flux through a closed surface is proportional to the net charge enclosed by that surface. Mathematically, it can be expressed as:
ΦE = Qenclosed / ε0
Where ΦE is the electric flux, Qenclosed is the net charge enclosed by the surface, and ε0 is the vacuum permittivity.
To effectively apply Gauss’s law, a Gaussian surface should be chosen based on the symmetry of the charge distribution. Some common shapes for Gaussian surfaces include spheres, cylinders, and planes.
Examples of Gaussian Surfaces
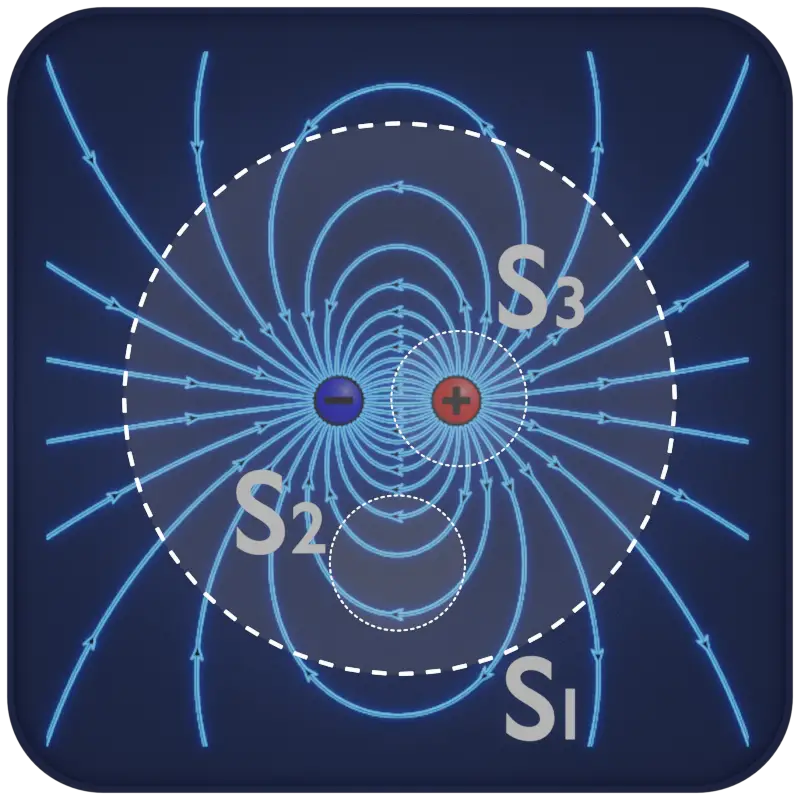
- Spherical Gaussian Surface: A spherical Gaussian surface is ideal for systems with radial symmetry, such as a point charge or a spherically symmetric charge distribution.
- Cylindrical Gaussian Surface: A cylindrical Gaussian surface is suitable for systems with cylindrical symmetry, like an infinitely long charged wire or a coaxial cable.
- Planar Gaussian Surface: A planar Gaussian surface is useful for systems with planar symmetry, such as an infinite charged plane or a parallel plate capacitor.
In conclusion, Gaussian surfaces play a vital role in simplifying complex electrostatic calculations and effectively applying Gauss’s law. By choosing an appropriate Gaussian surface based on the symmetry of the charge distribution, we can better understand electric fields and flux and explore various electrostatic phenomena.